At Numahub, training models is something we do more times in a week than having dinners with our better halves. While working with machine learning algorithms, especially the ones which use Gradient Descent for optimization, we often come across “step size”. If you are a Machine Learning enthusiast I am pretty sure you would have come across this term. I am hoping that by end of this article you should have a good idea of what it is and how should you set it.
Lets start with a quick recap of Gradient Descent. Gradient Decent is an optimization algorithm that excels at finding the best weights that minimize loss. If you are new to the term, please read my other article on “Gradient Descent”.
In Gradient Descent based optimization, you try to find the loss i.e. how bad your prediction was with a given set of weights. Then you try and find a way to minimize the error/loss.
Assume you have a convex loss function. Something like:
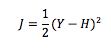
Where
J = Loss
Y = Actual values
H = Predicted Values (Example W*X)
W = Weights
X = Inputs
Then a simple plot of this function with Loss (J) on Y-axis and Weights (W) in X-axis would be:
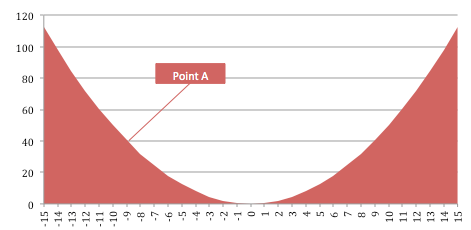
We are assuming a one-dimensional problem here.
Lets say we are at point A with some Loss J. We need to mutate the weights so that the loss reduces i.e. in this case increase the weights. The gradient method tells us to find the derivative of J at the point, which in this case happens to be:
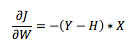
Further, The optimization algorithm says that mutate the weights in the direction where gradient is negative. In our example A, it would be moving towards right.
But then by what factor should we change the weights? This quantity - the amount, by which the weights should be modified, is called step size.
Typically, the weight update algorithm would be like:

Where
W = The current set of Weights
dJdW = Gradient of Loss with respect to Weight
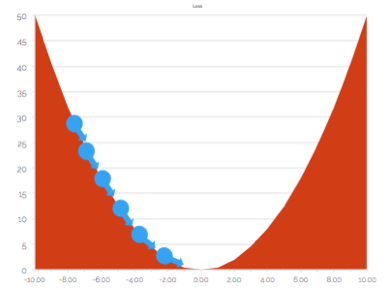
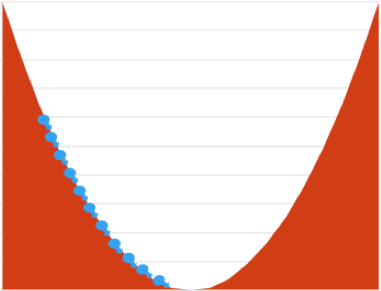
Step size decides how much you move while trying to go downhill i.e. minimize loss. The blue arrows above indicate the steps you take to reach the minimal loss.
Typically a new ML person would have these questions
- What should be the sign of step size?
- Should we have a large step size of small step size?
- What should be the size of step size?
The sign of step size should always be positive. The gradient calculated will decide the direction of movement. Step size should only be concerned with how much to move.loss_grad_2
Lets see the size/magnitude of step size. If you keep it too small, it will take more time to reach the best weights i.e. training will take more time.
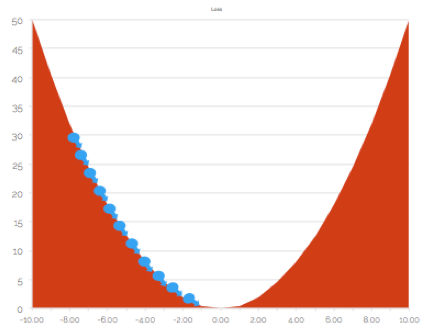
You might get tempted to have large step size as it will drastically reduce the training time. Well, this could be a bigger problem than you might imagine. If the size is large, you might overshoot the optimal position and keep oscillating between two sides of he valley.
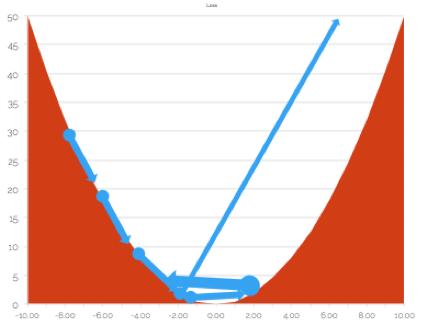
Further, there is a possibility that the gradient pushes you into infinity - thereby killing your entire training process.
Typically I suggest you start with step size as small as 1e-6. Then gradually start making it smaller.
If you end up Infinity or Not a Numeric errors at any point, that is an indication that your weights are too large
I have had good success with a step size of 1e-10 for some models I have trained in past.
Hope this was helpful.
